この間書いた「ヘックスマップのマス間の距離・・・つうかマス数の計算(正)」の続き。
今回は、ヘックスマップ上のスタート地点とゴール地点を与えてやって、自動で最短距離の経路を取得する方法を考えてみよう。
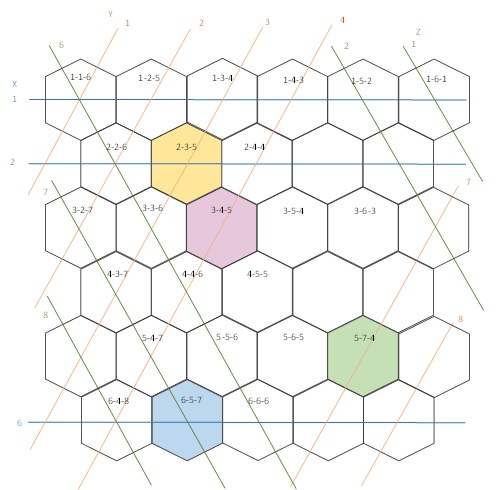
↑こういうマップをテストで使う。
青い線が X 軸、オレンジの線が Y軸、緑の線が Z 軸で、この軸の値を X-Y-Z のように並べてヘックスIDとする。
経路を決める方法としては、
・全ての経路を算出して、その中から最短のものを採用する(あるいは、人に選択させる)・最短の(あるいは任意の条件の)経路のみを算出する
という2パターンがあると思うが、全ての経路(あるいは任意の数の経路)を算出するのは大変なので、今回は最短経路を求めてみる。
で、最短経路をどうやって求めればいいかだが、とりあえず「目的地の方向へひたすら進む」という戦略を取ってみることにする。
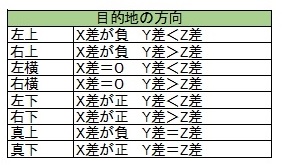
上の画像のような形で X,Y,Z 軸を決めると、ある任意のヘックスから見た目的地の方向は下の図のようになる。
要は、一歩一歩(1ヘックス進む毎に)目的地の方向を調べその方向へ進むということを繰り返すのだ。単純かつ確実。
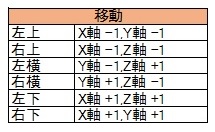
ちなみに、進める方向によって、元の X,Y,Z 軸の値に、下の表のように加減を行なう。
例えば、2-3-5 から 2-4-4 に移動するには右横に進めばいいので、2-3-5 の X 軸の値はそのままに、Y 軸の値に 1を足し、Z軸の値から 1を引けば 2-4-4 になるというわけ。
この間のエントリーに載せていた Perl スクリプトに、
# 経路選択$i = 0;for (;;) {# 方向を見極める$xd = $x2 - $x1; # X軸差$yd = $y2 - $y1; # Y軸差$zd = $z2 - $z1; # Z軸差$i++;# 方向によって、進むヘックスを決めるif ($xd == 0 && $yd > $zd) { # 目的地は真右$x1 = $x1;$y1 = $y1 + 1;$z1 = $z1 - 1;print "\[$i]目的地は真右\n";}elsif ($xd == 0 && $yd < $zd) { # 目的地は真左$x1 = $x1;$y1 = $y1 - 1;$z1 = $z1 + 1;print "\[$i]目的地は真左\n";}elsif ($xd < 0) {if ($yd == $zd) { # 目的地は真上(真上には行けないので、とりあえず右上に)$x1 = $x1 - 1;$y1 = $y1;$z1 = $z1 - 1;print "\[$i]目的地は真上(右上)\n";}elsif ($yd > $zd) { # この場合も右上$x1 = $x1 - 1;$y1 = $y1;$z1 = $z1 - 1;print "\[$i]目的地は右上\n";}elsif ($yd < $zd) { # 目的地は左上$x1 = $x1 - 1;$y1 = $y1 - 1;$z1 = $z1;print "\[$i]目的地は左上\n";}}elsif ($xd > 0) {if ($yd == $zd) { # 目的地は真下(真下には行けないので、とりあえず左下に)$x1 = $x1 + 1;$y1 = $y1;$z1 = $z1 + 1;print "\[$i]目的地は真下(左下)\n";}elsif ($yd < $zd) { # この場合も左下$x1 = $x1 + 1;$y1 = $y1;$z1 = $z1 + 1;print "\[$i]目的地は左下\n";}elsif ($yd > $zd) { # 目的地は右下$x1 = $x1 + 1;$y1 = $y1 + 1;$z1 = $z1;print "\[$i]目的地は右下\n";}}# もうゴール?if ($x1 == $x2 && $y1 == $y2 && $z1 == $z2) {print "\[$i]ゴールです!$x1-$y1-$z1\n";last;}else {print "\[$i]経路=$x1-$y1-$z1\n";}}
こういう処理を足して実行してみる。
上の図の 2-3-5(黄色いヘックス)から 5-7-4(緑のヘックス)への経路を作成させてみると、
$ ./hex_dist2.pl開始位置=2-3-5終了位置=5-7-4最短距離=4[1]目的地は右下[1]経路=3-4-5[2]目的地は右下[2]経路=4-5-5[3]目的地は右下[3]経路=5-6-5[4]目的地は真右[4]ゴールです!5-7-4
お、ちゃんと最短距離で正しく経路を作成してるぞ。
今度は逆方向に、6-5-7(青色のヘックス)から 2-3-5(黄色いヘックス)に向かう経路を作成させる。
$ ./hex_dist2.pl開始位置=6-5-7終了位置=2-3-5最短距離=4[1]目的地は真上(右上)[1]経路=5-5-6[2]目的地は左上[2]経路=4-4-6[3]目的地は真上(右上)[3]経路=3-4-5[4]目的地は左上[4]ゴールです!2-3-5
ばっちりやん。
六角形のマスなので、真上や真下には動けないから、とりあえず右か左に一旦進んで、ようはジグザグに行くしかないのでこういう動きになる。
今回は、
・マップの端に達した(最短距離を取るので今回はあり得ないんだけど)・障害物がある(マップ上に配置された岩や沼など)・コマの向きの概念(方向転換しないと、向いている方向にしか進めない)
というようなケースには非対応なので、今後はこの辺のロジックを考えていくかな。
(連続する障害物をどう避けていくか・・・とか)

コメントする