この間書いた「ヘックスへの最短経路の自動計算」の話で、真上のヘックスに対してジグザグに進んでいく案を示したのだが、それに対して「移動するヘックス数は同じでも、それでは運動量が大きくなりすぎるので最短経路とはいえない」という意見をいただいた。
この手のヘックスマップの場合、例えば右横に行こうとすると「右に必要なだけ回転して進路を変える」という動作が必要になる。そして、ジグザグに動くということは、「右に向きを変える」「1つヘックスを進む」「左に向きを変える」「1つヘックスを進む」という具合に、間に向きを変える動きが入るので、最短経路とはいえないということだ。
なぜかというと、「向きを変える」という動きに、例えば「1ヘックス進む」という動きと同じ運動量が想定されている場合が多い。
つまり、ジグザグに「右、左」と進んだ時は、2移動量ではなく4移動量分の運動量が消費されるというわけだ。
なるほど。
例えば、前回の話で使用したマップであれば、6-5-7 から 2-3-5 に向かうのに、
6-5-7→5-5-6→(L)→4-4-6→(R)→3-4-5→(L)→2-3-5
と進む場合、移動量は4ではなく(5-5-6 へのまっすぐ進んだとして)間に3回の方向転換を含むので、7である・・・という考え方やね。(L は左転換、R は右転換)
なので、本当の最短経路は、できるだけ斜めに突っ切って、途中で方向転換してまた斜めに目標に向かう、
6-5-7→5-5-6→4-5-5→(L)→3-4-5→2-3-5
であると。これであれば、4-5-5 から 3-4-5 に進む時に1回だけ方向転換をすればいいので、移動量は5ですむと。
これは、「大戦略」などのメジャーなゲームで採用されているパターンのようだ。つまり「コマの向き」がヘックスの「辺」に向かっているということだね。
いや、俺も Windows 3.1 の頃に「大戦略」買ってやったことあるけど(IIIかなあ?)、すぐ飽きちゃったので記憶にまったく残ってないのだ(^^;なので、上記のような指摘をいただいた時、「???」なのであった。
今回、俺が想定しているゲームは、国際通信社から出ている「WORLD TANK BATTLES」(ワールド タンク バトルズ~小さな戦車の大戦車戦!~)である。
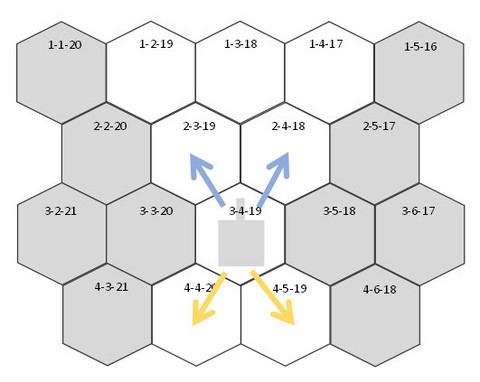
このゲームは、上の図のように「コマの向き」がヘックスの「頂点」なのだ。そして、その頂点の左右にあるヘックスには「方向転換無し」で進めるのである。(青い矢印)
後退の場合も、同じように後ろの頂点の左右には「方向転換無し」で進める。(黄色い矢印)
つまり、
6-5-7→5-5-6→4-4-6→3-4-5→2-3-5
も、
6-5-7→5-5-6→4-5-5→3-4-5→2-3-5
も、同じ「移動量4(運動量4)」なのである。(L や R の転換がない)
もちろん、上の図で言うと、3-4-19 から 3-5-18 に向かおうとすると、右に1頂点分回転しないといけないので、そこで+1移動量となるが。
この前提を提示していなかったので色々混乱を呼んでしまった。
ただ、「可能な限り斜めに向かい、1回だけ方向転換して更に斜めに目標地点に向かう」という経路の取り方は、障害物の迂回経路を自動作成するのに使えそうである。
ということで、次回はこの斜めコースの自動作成方法について考えてみよう。

コメントする