前回書いたように、なるべく方向転換をしない経路(スタート地点、ゴール地点が向かい合う対角の頂点である平行四辺形の2辺を辿るコース。つまり2パターンある)を自動作成するためには、その各パターン一つだけの方向転換点をまず算出しなくてはならない。
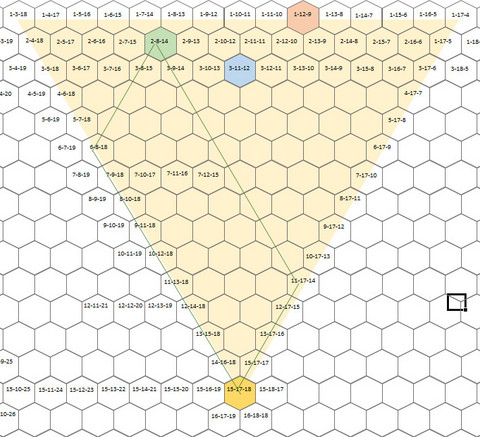
上の例では、スタート地点が 15-17-18(黄色のヘックス)、ゴール地点が 2-8-15(緑のヘックス)だが、この場合の方向転換点は、コマの進行方向(この場合、ヘックスの 0時方向)の右と左に向かう2パターンがあり、それぞれ X,Y,Z軸の値が以下の計算で求められる。
※スタート地点を(A)、ゴール地点を(B)とする。
X = X(A) - (Z(A) - Z(B)) = 15 - (18 - 14) = 11
Y = Y(A) = 17
Z = Z(B) = 14
X-Y-Z = 11-17-14
<左に向かうコースの転換点の座標>
X = X(A) - (Y(A) - Y(B)) = 15 - (17 - 8) = 6
Y = Y(B) = 8
Z = Z(A) = 18
X-Y-Z = 6-8-18
実際の図に照らし合わせてみると、ちゃんと合っているのが確認できる。
その他のゴールの場合も、例えば 3-11-12(青)に向かう場合の転換地点は 9-17-12(右)と 9-11-18(左)で上記の計算方法のとおりで、ゴールが 1-12-9(橙)の場合の転換地点、6-17-9(右)、10-12-18(左)の場合もそうである。
進路の決め方としては、
1.まず、転換地点を算出。2.スタートからその転換地点までの最短経路を作成3.その転換地点からゴールまでの最短経路を作成
となる。
例えば、「スタートからその転換地点までの最短経路」であれば、前回作った「目的地の方向へひたすら進む」というプログラムをそのまま使えば良いし、「転換地点からゴールまでの最短経路」も同じである。
さて、ゴールが上図で薄い黄色で塗った三角形の内側であればこの計算でいけることが実証できた。
次は、三角形の部分とは別の方向にゴールがある場合、この計算式でいいのか?別の計算式はどういう内容か・・・といった辺りを考えてみることにする。
今日はもう肩(五十肩)が痛いので寝るよ(笑)

コメントする