帰りの電車で考えて、やっと解決した。
さっきは六角形の位置情報を X, Y の 2軸で考えていたのが敗因だったな。
結局、
・各マスの位置を、X,Y,Z の 3軸で表現する。・移動元と移動先の X,Y,Z の各差(絶対値)の中で一番大きな値を採用。
というやり方で最短距離が取れるわ。
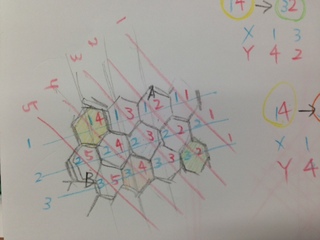
ちょっとわかりづらいと思うが、上の写真を見てちょ。
(そのうち、Excel かなんかで綺麗にまとめる予定)
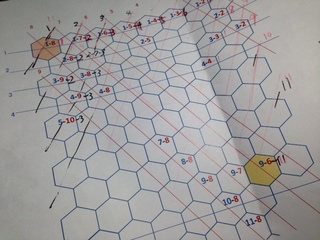
横の軸が X軸、左から右に降りていく軸が Y軸、右から左に降りていく軸を Z軸として、一番左上のマスに 1-8-1 という位置情報を与える。X=1,Y=8,Z=1 だ。
同じルールで、右下の方にある黄色いマスに位置情報を与えると 9-6-11 となる。X=9,Y=6,Z=11 の位置だ。
で、X,Y,Z の差をそれぞれ絶対値で求めると、8,2,10 となるよね。この中で一番大きな数字、つまり 10 がこの二点間の距離(マス数)なんだね。
逆方向もバッチリよ。
一番右上のマス(1-1-8)から、黄色いマス(9-6-11)までの距離(最短距離)は 8 である。
ほんじゃ、ホントに 8 になるか計算してみよう。Z,Y,Z の差の絶対値がそれぞれ 8,7,3 だから、バッチリ 8 で正解やん!
ふむふむ。これでどうにかなりそうやな。
Perl で書けばこんな感じ。
#!/usr/bin/perlprint "開始位置=";$start = <STDIN>;chomp $start;print "終了位置=";$end = <STDIN>;chomp $end;if ($start =~ /^(\d+)\-(\d+)\-(\d+)$/) {($x1, $y1, $z1) = ($1, $2, $3);}else {print "ERROR\n";exit();}if ($end =~ /^(\d+)\-(\d+)\-(\d+)$/) {($x2, $y2, $z2) = ($1, $2, $3);}else {print "ERROR\n";exit();}@dist = (abs($x1 - $x2), abs($y1 - $y2), abs($z1 - $z2));@dist = sort {$a <=> $b} @dist;print "最短距離=" . $dist[2] . "\n";exit();
実行してみたら、ばっちり正しい距離が出た。
$ ./hex_dist.pl開始位置=1-8-1終了位置=9-6-11最短距離=10
ふむ。じゃ、戦車戦ボードゲームサポートプログラム(笑)に実装するか。