今回、二点間の緯度・経度から距離を出すプログラム書いたことで、三角関数とか久しぶりに触れたのでメモっとく。
まず、地球の半径、円周について。
地球の極半径は6,356.752kmで、赤道半径は6,378.137kmだけど、今回は経度 1度あたりの距離の話なので赤道半径を「地球の半径」と考える。円周は、6,378.137 × 2 × 3.1415(近似値)で 40,073.834km。よく言われる「約 4万km」だよね。
この数値から、赤道部(緯度 0度)では、経度 1度あたりの距離は、円周を 360度で割ればいいので、40,073.834km ÷ 360度で 111.3162km。これも、「約 111km」って表現されてるのを聞いたことがある人もいるだろう。
ところで、緯度 1度あたりの距離は単純である。
極半径 6,356.752kmを元に円周をもとめ、360度で割るだけだ。6,356.752km × 2 × 3.1415 ÷ 360で 110.94297km。地球は自転の関係で赤道半径の方が大きいので、赤道部の経度 1度より短いが、まあ、約 111km だね。厳密に距離を出したのなら、緯度 1度の距離は 110.94297 を使おう。そして緯度 1度は、地球を縦方向(北極、南極を結ぶ線で)に 360等分したものなので、1度あたりの距離は経度がどこであれ変わらない。
問題は、赤道部以外の経度 1度あたりの距離である。
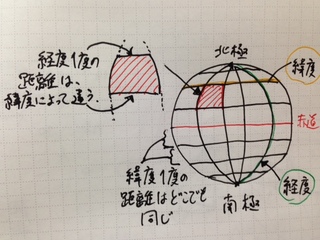
緯度というのは地球を赤道に並行に輪切りにしたものである。つまり、極に近づくほど輪切りにされた円周は短くなる。輪っかが小さくなっていくからな。
そうすると、経度 1度は常にその円周を 360分割したものだから、当然極に近づくほど 1度あたりの距離は短くなっていく。
計算方法は後にして、緯度の違いでどの程度経度 1度あたりの距離が変わってくるか計算すると、
- 赤道(緯度 0度) 約111km
- 東京(緯度35度) 約 91km
- 北海道(緯度44度) 約 80km
- 鹿児島(緯度31度) 約 95km
- シベリア(緯度70度) 約 38km
- ニュージーランド(緯度-45度) 約 79km
となる。
自宅が経度133度にあって、目的の店は経度134度にあるよ・・・って時に、シベリアなら 38km車で走れば着くが、日本では 91kmも走らないといけないということだ。
だから、物件の緯度・経度で位置を管理し、ある物件から別の物件までの距離を計算するとき、日本国内のみを考えたサービスなら「経度 1度あたりの距離は東京の 91kmを固定でもっておいても、ギリギリなんとかなるかな」という感じだけど、世界を相手にするのなら、きちんと緯度から経度 1度あたりの距離を毎回動的に計算してやらないとどうしようもない・・・ということがわかる。
そこで、どうやって「ある緯度の経度 1度あたりの距離を計算する」かだ。
何がわかれば 1度あたりの距離が出るかと言うと「その緯度で地球を輪切りにした時の円周」である。
赤道部の円周は 40,073.834kmだから、360で割って 1度あたりの距離は 111kmと出る。
東京のところで輪切りをした円の半径は約5224.66kmである。なので、5224.66 × 2 × 3.1415 で 32,810.864km が円周だ。これを 360で割ると、経度 1度あたりの距離は 91.141288km となるわけだ。
この中で、計算しないとわからないのはなんだろう?
そう、輪切りにした円の半径である。これがわからないと円周も計算できない。
その半径を求めるために、やっと、三角関数の登場である。
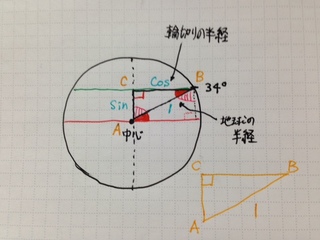
輪切りにした円の半径は、輪切りにした面の中心点から地球の中心点に伸びる線(高さ)と、輪切りにした面(底辺)、地球の中心点からその緯度の地表に伸びた線(斜線)で構成される直角三角形の底辺の長さ(コサイン)です。(正確には「長さ」ではなく「斜辺に対する底辺の比」だけど)
C点の角度が直角なので、B点の角度がわかれば、斜辺を 1とした時の底辺の長さが出ます。これが三角関数やね。
Perl では、コサインの計算をするために cos という関数が用意されてる。
この関数に、B点の角度をラジアン値で与えてやれば斜辺を 1とした時の底辺の長さが出るのだ。
新しい言葉が出てきたけど(^^;>ラジアン
ラジアン値というのは、例えばホールで買って来たケーキを切り分けるじゃん。三角形の形(外側の辺は直線ではなく弧)に。その時の外側の円の部分(弧)の長さと、直線部の一辺(半径)の長さが同じになる時の直線二辺をつなぐ部分の角度を 1とした時の値である。
言葉で書くとわかりづらいと思うので、ラジアンなんかもう忘れたわ!という人は、各自ググってください(笑)
ちなみに、1ラジアンは約 57.296度ね。
さらに言うと、1ラジアン時の弧の長さを 1(半径と同じ)とすると、半円(角度 180度)のラジアン値は約 3.1415ということになる。半円の円周は半径の3.1415倍だからな。ラジアン値も 3.1415倍されるわけ。
ということで、緯度 35度の場合のラジアン値の計算は、35度 ÷ 180度 × 3.1415(最大のラジアン値)で、約 0.610847ラジアンとなる。
これを、cos 関数に突っ込むと、0.819162505153376という数字が返ってくる。斜辺 1とした時の底辺が 0.819162505153376というわけだ。
これで、緯度35度地点で輪切りにした円の半径が出るね。地球の半径(斜辺)との関係が 1:0.819162505153376 だから、6,378.137(地球の半径):x で、x の値は約 5,224.7306 となる。故に円周は約 32,811.397lmとなり、360で割れば約 91.142519km となるというわけである。(上の方で計算している値と微妙に違うんだけど(^^;計算につかった数値の桁数が違ってるもんで、その誤差だから許して(^^;)
Perl でプログラムを書くと、
$pi = 3.1415926535898; # 円周率近似値
$lt = 34.410280; # 場所1の緯度(10進)横川駅
$er = 6378.137; # 地球の半径(km)
$cf = cos($lt / 180 * $pi) * 2 * $pi * $er; # 任意の緯度の円周(km)
$kd = $cf / 360; # 経度 1度あたりの km。
こうね。
で、厳密に言うと、緯度によって地球の半径も変わってくるので、毎回 6,378.137を使うのはどうなの?緯度の値が大きくなる(南半球であればマイナス方向に大きくなる)と極半径 6,356.752 に近くなるよね!・・・みたいな話もあるんだけど、あなたの作ろうとしているプログラムでそこまでの精度がいる?そもそも、物件データとして登録している緯度・経度も、そんな誤差が許されないほどの精度なの?ってことだよ。
もちろん、地球がきれいな楕円であれば任意の緯度地点での地球の半径も計算出来ると思うけど、そこまでの精度は現実には不要なので赤道半径を常に使ってもかまわないだろう。どうしても厳密な計算が必要っていう人は、その具体的な例を上げてみてくれ。
ないよな?(笑)
ということで、数十年ぶりの三角関数のお勉強は、これにて終了(笑)
※高校生の時のわずかな記憶と、適当にググった内容をもとに書いています。多分、俺の高校時代と考え方が変わってる点や誤解からの間違いなんかもあると思いますがご容赦を>数学マスターな皆様